Molecular Electronics
When the field Molecular Electronics was emerging at the end of the last century its main drive was towards building new devices for applications in information and sensor technology. This still is important motivation driving the field.
However, it soon became clear that Molecular Electronics is much more than this. It is a field of fundamental sciences, where Chemistry, Surface and Condensed Matter Experts collaborate in order to understand fundamental processes at interfaces in and out of equilibrium. Questions range from the flow of charge and heat around single atoms in molecular switches up to biological scales, where sticking of specific viruses can be gate-controlled on certain semi-conductor surfaces.
Enormous challenges exist in the field concerning method development but also with respect to analyzing fascinating experiments on single molecule or even single atom transport. Activities in our group concern both directions, supported by numerous international collaborations.
Molecular Instabilities and Magnetism
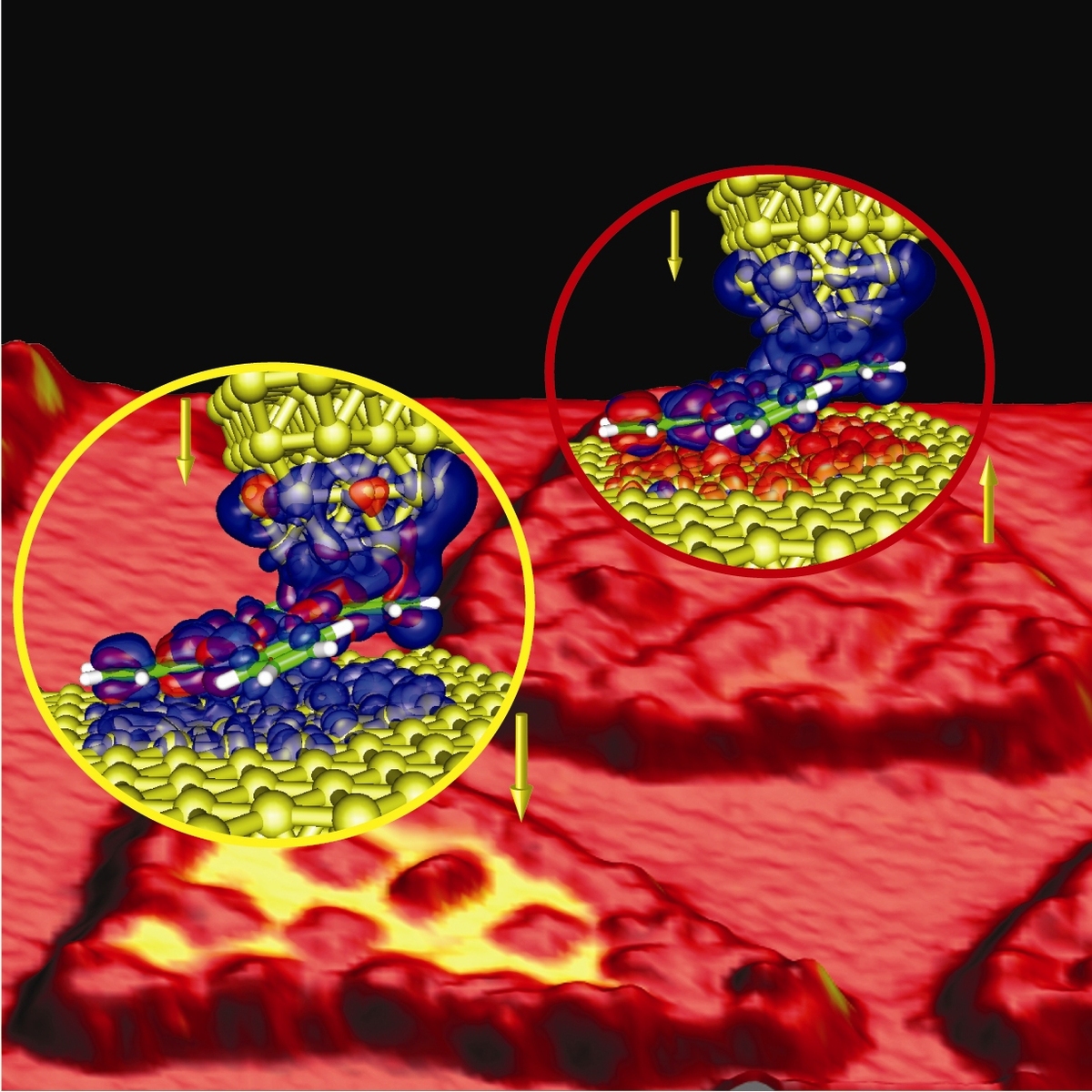
A very distinct feature of molecules, that makes them very special as compared to, e.g., quantum dots familiar from semi-conductor devices, originates from their symmetries, e.g. related to space groups. Roughly speaking, such symmetries can produce degeneracies which in turn lead to the competition of ground states, say magnetic vs non-magnetic ones. As a consequence, by proper chemical design a molecular structure can be tuned close to an instability which then can be addressed experimentally, say by a gate voltage or strain. In this way, a molecular bistability can be constructed, that can exhibit, e.g., a switchable Kondo-effect.
In close collaboration with experimental groups, we study such molecular switches theoretically with methods comprising the density functional theory (DFT) and non-equilibrium Green's functions. In addition, also more advanced electronic structure machinery, like the GW-method, is being used.
Density Functional Theory for Transport Applications
The application of density functional theory (DFT) to transport problems has a long history in the field of Molecular Electronics. The DFT-technology is so important, because it can connect the molecular structure to its observable properties, which often are sensitive to changing just a single atom. DFT-transport theories rely upon two central ingredients. Future improvements require work in both directions and we are active there.
Fundamental Aspects and Functionals
At the heart of any DFT-calculation is the density functional. All DFT-calculations rely upon certain approximations of this functional, the best known one being the local density approximation (LDA). We aim at the better understanding and, in particular, also at improving existent functionals with a special emphasis on the development of post-DFT procedures like the GW-technology for applications in Molecular Electronics.This fundamental research can be expected to have broad impact in all nano-sciences that rely upon ab-initio calculations.
Nonequilibrium Green's Function Approach: AitransS
The results of any first principles calculation need to be converted into transport information, like transmission functions, charge and heat conductances etc.. To this end we employ the nonequilibrium Green's functions approach. Our particular methodology is implemented in a transport module -- AitransS -- that currently is running with standard DFT-codes TURBOMOLE and FHI-aims.
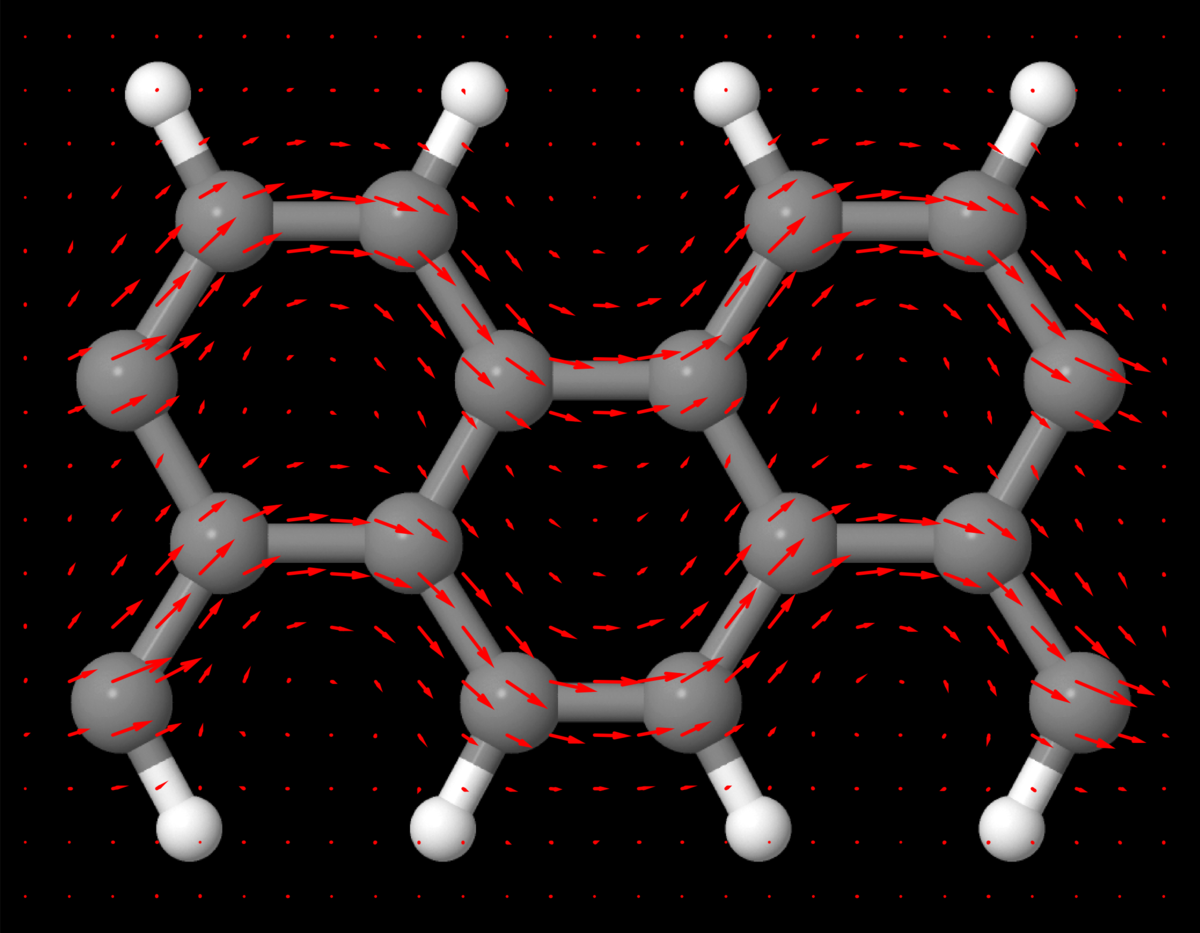
Improvements and extensions of this transport module are continuously under way. This includes the calculation of local current densities, orbital magnetism in non-equilibrium and the transport of heat.
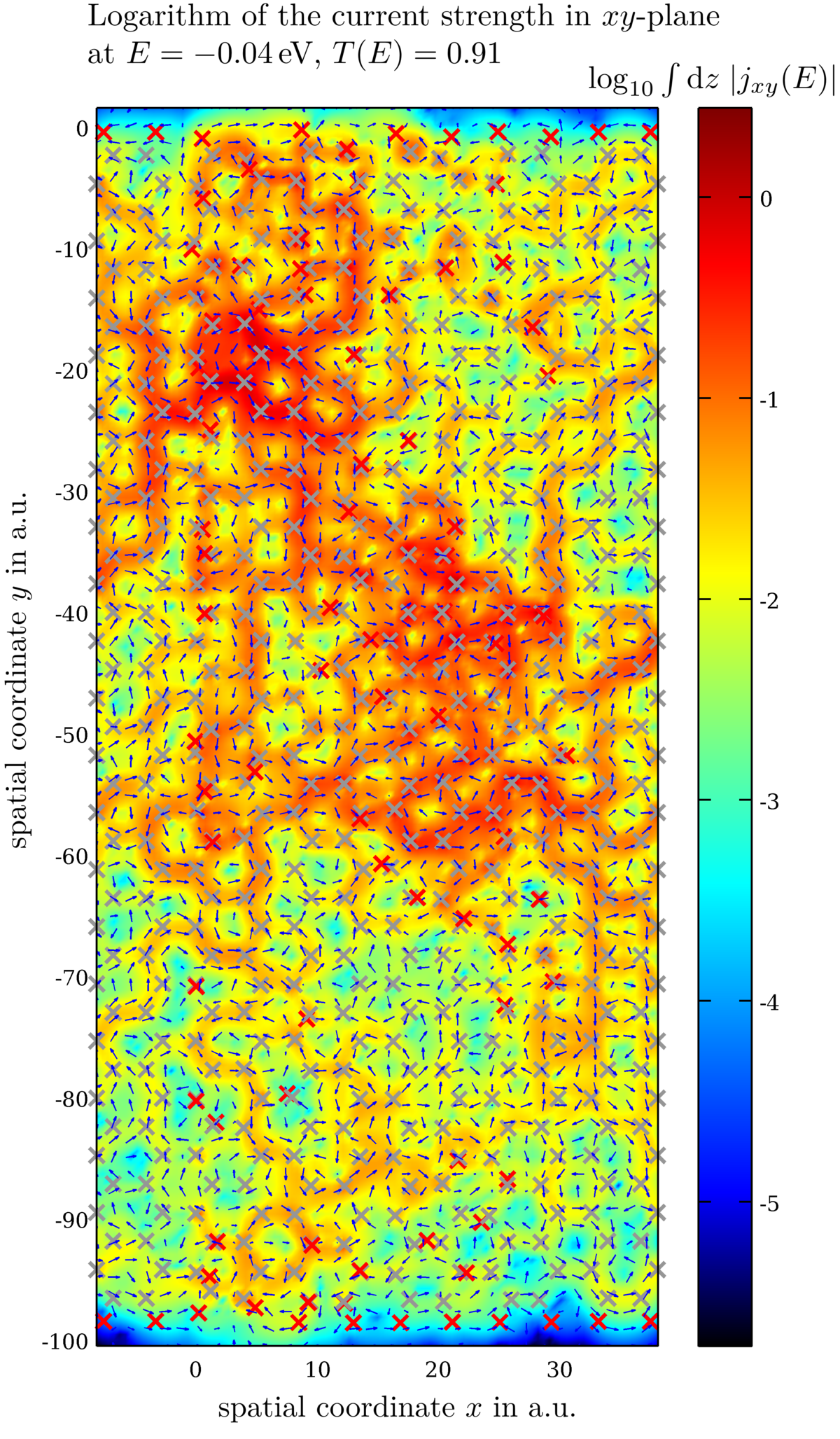
Current pattern in large functionalized graphene flakes
Using our transprt tool, we also investigate the effect of functionalization on conductance and the current pattern through large mesoscopic flakes. Usually these currents vary greatly on microscopic length-scales. Our DFT-approach includes effects like lattice distortion, e.g. strain, and cross-talk between different impurities.