Complex order in quantum materials

nematicity, time-reversal symmetry breaking, vestigial order ...
Strain tuning systems with nematic order, R. Willa, M. Fritz, and J. Schmalian, Physical Review B 100, 085106 (2019).
Phase diagrams in states of vestigial order, R. M. Fernandes, P. P. Orth, and J. Schmalian, Annual Review of Condensed Matter Physics 10, 133 (2019).
anisotropic transport in the vestigial phase of a nematic superconductor, M. Hecker and J. Schmalian, npj Quantum Materials 3, 196801 (2018).
Phase diagram of 122 iron-based superconductors with nematic order and fluctuations, R. M. Fernandes, A. V. Chubukov, and J. Schmalian, Nature Physics 10, 97 (2014).
Raman response of 122-iron-based systems, experiment and theory for spin-fluctuation induced Ising nematicity, F. Kretzschmar, et al. Nature Physics, 12, 560 (2016).
Anisotropic In-Plane Resistivity in the Nematic Phase of the Iron Pnictides, R. M. Fernandes, E. Abrahams, and J. Schmalian, Physical Review Letters 107, 217002 (2011).
Valence bond state of vestigial order in different lattices, R. M. Fernandes, P. P. Orth, and J. Schmalian, Annual Review of Condensed Matter Physics 10, 133 (2019).

Our research activities in the theory of superconductivity are partly supported by the  DFG transregional collaborative research center TRR-288. 

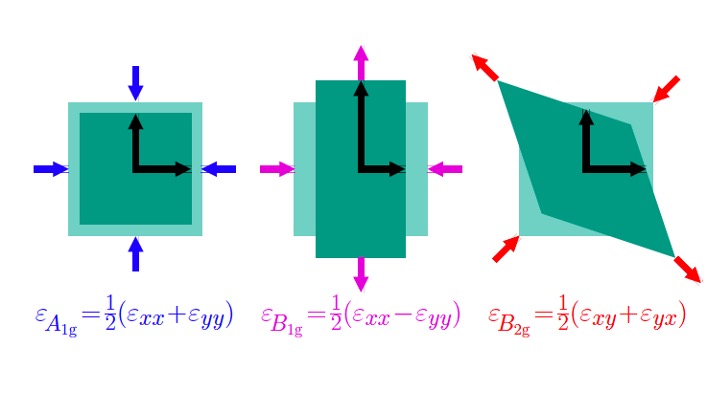
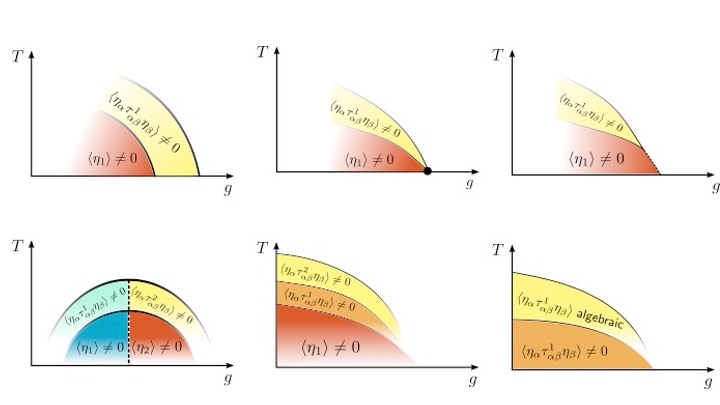
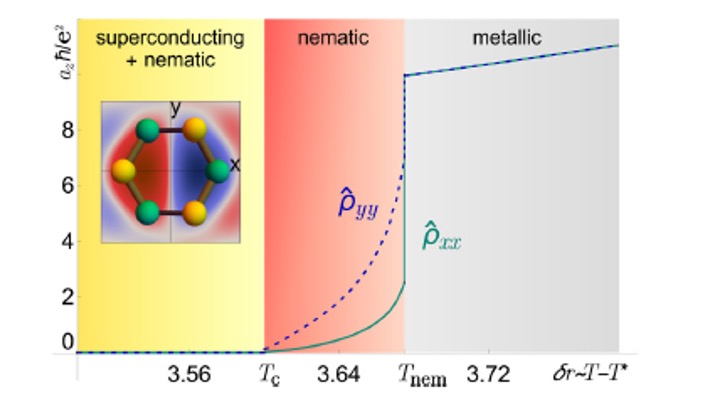
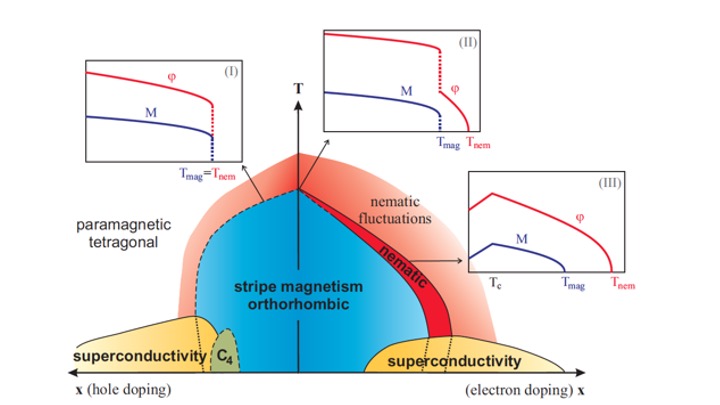
A hallmark of the phase diagrams of quantum materials is the existence of multiple electronic ordered states, which, in many cases, are not independent competing phases, but instead display a complex intertwinement. A particular realization of such intertwined orders occurs when a primary phase, characterized by a multi-component order parameter, gives rise to  a fluctuation-driven vestigial phase that is characterized by a composite order parameter. This concept has been widely employed to elucidate nematicity in iron-based and cuprate superconductors. This notion also applied to a variety of phases such as nematic superconductivity or time reversal symmetry of multi-component superconductors. Electronic states with scalar and vector chiral order, spin-nematic order, Ising-nematic order, time-reversal symmetry-breaking order, and algebraic vestigial order emerge from one underlying principle.  

Return to the research group - strongly correlated electrons.

Selected Publications:

  • Z3-vestigial nematic order due to superconducting fluctuations in the doped topological insulators NbxBi2Se3 and CuxBi2Se3, C.-w. Cho, J. Shen, J. Lyu, O. Atanov, Q. Chen, S. H. Lee, Y. S. Hor, D. J. Gawryluk, E. Pomjakushina, M. Bartkowiak, M. Hecker, J. Schmalian, and R. Lortz, Nature Communications 11, 3056 (2020). https://arxiv.org/abs/1905.01702
  • Intertwined Vestigial Order in Quantum Materials: Nematicity and Beyond, R. M. Fernandes, P. P. Orth, and J. Schmalian, Annual Review of Condensed Matter Physics 10, 133 (2019). https://arxiv.org/abs/1804.00818
  • Enhanced nematic fluctuations near an antiferromagnetic Mott insulator and possible application to high-Tc cuprates, P. P. Orth, B. Jeevanesan, R. M. Fernandes, and J. Schmalian, npj Quantum Materials 4, 4 (2019). https://arxiv.org/abs/1703.02210
  • Strain tuning and anisotropic spin correlations in iron-based systems, R. Willa, M. Fritz, and J. Schmalian, Physical Review B 100, 085106 (2019). https://arxiv.org/abs/1904.05583
  • Soft phonons reveal the nematic correlation length in Ba(Fe0.94Co0.06)2As2 F. Weber, D. Parshall, L. Pintschovius, J.-P. Castellan, M. Kauth, M. Merz, Th. Wolf, M. Schütt, J. Schmalian, R. M. Fernandes, and D. Reznik, Physical Review B 98, 014516 (2018). https://arxiv.org/abs/1806.05581
  • Vestigial nematic order and superconductivity in the doped topological insulator CuxBi2Se3, M. Hecker and J. Schmalian, npj Quantum Materials 3, 196801 (2018). https://arxiv.org/abs/1712.07523
  • Elastic coupling and spin-driven nematicity in iron-based superconductors. U. Karahasanović and J. Schmalian, Physical Review B 93, 064520 (2016). https://arxiv.org/abs/1512.04861
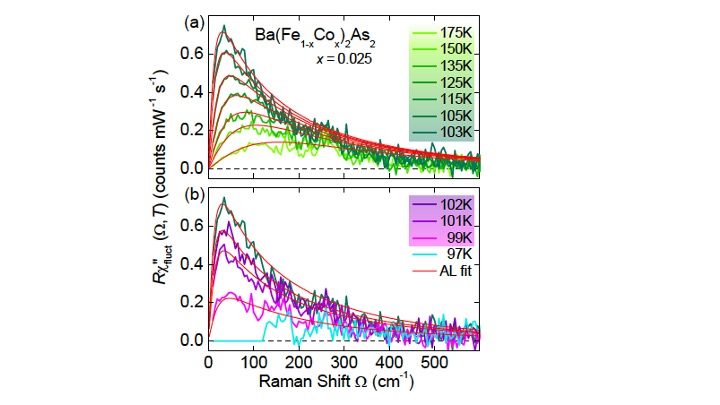
  • Critical spin fluctuations and the origin of nematic order in Ba(Fe1-xCox)2As2, F. Kretzschmar, T. Böhm, U. Karahasanović, B. Muschler, A. Baum, D. Jost, J. Schmalian, S. Caprara, M. Grilli, C. Di Castro, J. G. Analytis, J.-H. Chu, I. R. Fisher, and R. Hackl, Nature Physics, 12, 560 (2016). https://arxiv.org/abs/1507.06116
  • Nematic resonance in the Raman response of iron-based superconductors, Y. Gallais, I. Paul, L. Chauviere, J. Schmalian, Physical Review Letters 116, 017001 (2016). https://arxiv.org/abs/1504.04570
  • Manifestation of nematic degrees of freedom in the Raman response function of iron pnictides, U. Karahasanović, F. Kretzschmar, T. Böhm, R. Hackl, I. Paul, Y. Gallais, and J. Schmalian, Physical Review B 92, 075134 (2015). https://arxiv.org/abs/1504.06841
  • Origin of nematic order in FeSe, A. V. Chubukov, R. M. Fernandes, and J. Schmalian, Physical Review B Rapid Communications 91, 201105(R) (2015). https://arxiv.org/abs/1504.02315
  • What drives nematic order in iron-based superconductors? R. M. Fernandes, A. V. Chubukov, and J. Schmalian, Nature Physics 10, 97 (2014). https://arxiv.org/abs/1312.6085
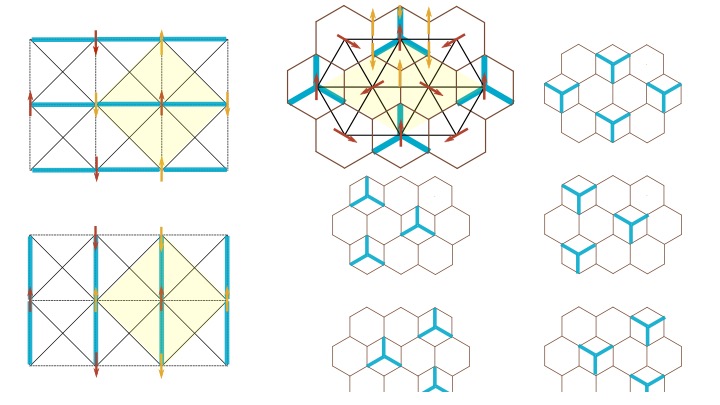
  • Emergent criticality and Friedan scaling in a two-dimensional frustrated Heisenberg antiferromagnet, P. P. Orth, P. Chandra, P. Coleman, and J. Schmalian, Physical Review B 89, 094417 (2014). Editor’s suggestion https://arxiv.org/abs/1312.2596
  • Scaling between magnetic and lattice fluctuations in iron-pnictide superconductors, R. M. Fernandes, A. E. Böhmer, C. Meingast, J. Schmalian, Physical Review Letters 111, 137001 (2013). https://arxiv.org/abs/1306.0521
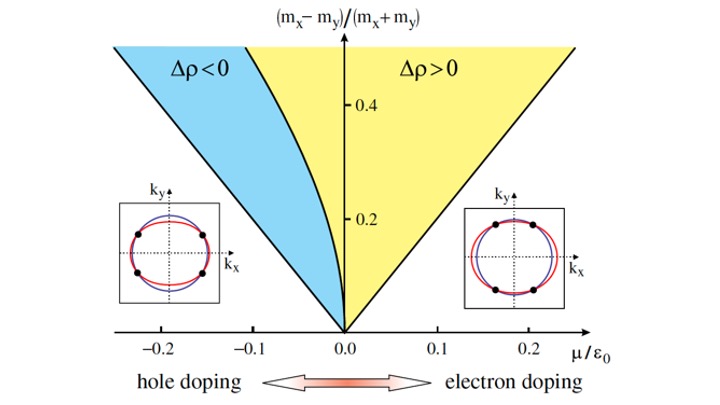
  • Sign-reversal of the in-plane resistivity anisotropy in hole-doped iron pnictides, E. C. Blomberg, M. A. Tanatar, R. M. Fernandes, I. I. Mazin, B. Shen, Hai-Hu Wen, M. D. Johannes, J. Schmalian, and R. Prozorov, Nature Communications 4, 1914 (2013). https://arxiv.org/abs/1202.4430
  • Manifestations of nematic degrees of freedom in the magnetic, elastic, and superconducting properties of the iron pnictides, R. Fernandes, J. Schmalian, Superconductor Science and Technology 25, 084005 (2012). https://arxiv.org/abs/1204.3694
  • Preemptive nematic order, pseudogap, and orbital order in the iron pnictides, R. M. Fernandes, A. V. Chubukov, J. Knolle, I. Eremin, and J. Schmalian, Physical Review B 85, 024534 (2012). https://arxiv.org/abs/1110.1893
  • Emergent Critical Phase and Ricci Flow in a 2D Frustrated Heisenberg Model, P. P. Orth, P. Chandra, P. Coleman, and J. Schmalian, Physical Review Letters 109, 237205 (2012). https://arxiv.org/abs/1312.2596
  • Unbinding of Giant Vortices in States of Competing Order, J. M. Fellows, S. T. Carr, C. A. Hooley, and J. Schmalian, Physical Review Letters 109, 155703 (2012). https://arxiv.org/abs/1205.1333
  • Anisotropic In-Plane Resistivity in the Nematic Phase of the Iron Pnictides, R. M. Fernandes, E. Abrahams, and J. Schmalian, Physical Review Letters 107, 217002 (2011).    https://arxiv.org/abs/1105.3906
  • Effects of Nematic Fluctuations on the Elastic Properties of Iron Arsenide Superconductors, R. M. Fernandes, L. H. VanBebber, S. Bhattacharya, P. Chandra, V. Keppens, D. Mandrus, M. A. McGuire, B. C. Sales, A. S. Sefat, and J. Schmalian, Physical Review Letters 105, 157003 (2010). https://arxiv.org/abs/0911.3084​​​​​​​
  • Conductivity of electronic liquid-crystalline mesophases, Rafael M. Fernandes, R.M., Schmalian J., and Westfahl Jr. H., Phys. Rev. B 78, 184201 (2008). https://arxiv.org/abs/0809.3266
  • Emergent symmetry and dimensional reduction at a quantum critical point, J. Schmalian and C.D. Batista, Physical Review B 77, 094406 (2008). https://arxiv.org/abs/0710.1376
  • Geometric frustration and dimensional reduction at a quantum critical point, C. D. Batista, J. Schmalian, N. Kawashima, P. Sengupta, S. E. Sebastian, N. Harrison, M. Jaime, I. R. Fisher, Physical Review Letters 98, 257201 (2007).  https://arxiv.org/abs/cond-mat/0608703